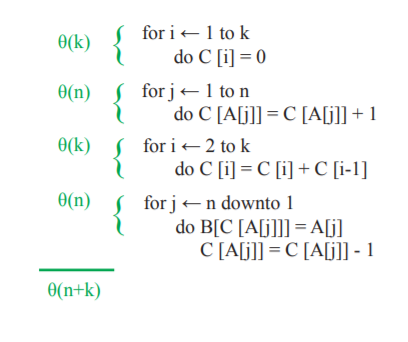Counting Sort
Ins and Outs of Counting sort algorithm, If we stick to comparison-based sorting methods cannot do better than Ω(n log n).
Introduction
If we stick to comparison-based sorting methods cannot do better than Ω(n log n), Comparison-based Lower Bounds for Sorting
- It operates by counting the number of objects that have each distinct key values
- Integer sorting algorithm: we assume the values to be integers
- Using arithmetic on those counts to determine the positions of each key value in the output sequence.
- It is only suitable for direct use in situations where the variation in keys is not significantly greater than the number of items
- It can be used as a subroutine in radix sort
- Because counting sort uses key values as indexes into an array, it is not a comparison based algorithm, so linearithmic running time can be reduced.
arr = [6, 3, 9, 10, 15, 6, 8, 12, 3, 6]
def return_max(arr):
for i in range(len(arr)-1):
if (arr[i] > arr[i+1]):
arr[i], arr[i+1] = arr[i+1], arr[i]
return arr[-1]
return_max(arr)
#collapse-hide
def counting_sort(arr):
max_arr = return_max(arr)
count_arr = []
res_arr = []
for i in range(max_arr+1):
count_arr.append(0)
for i in range(len(arr)):
count_arr[arr[i]] += 1
i = 0
while(i < len(count_arr)):
if(count_arr[i] > 0):
res_arr.append(i)
count_arr[i] -= 1
i = 0
i += 1
return res_arr
counting_sort(arr)
#collapse-hide
def counting_sort_without_duplicates(arr):
max_arr = return_max(arr)
count_arr = []
res_arr = []
for i in range(max_arr+1):
count_arr.append(0)
for i in range(len(arr)):
count_arr[arr[i]] += 1
for i in range(len(count_arr)):
if count_arr[i] > 0:
res_arr.append(i)
count_arr[i] -= 1
return res_arr
counting_sort_without_duplicates(arr)
Time Complexity [Worst Case]: $O(n+k)$, where k is the range of the non-negative key values.
Space Complexcity [Worst Case]: $O(n+k)$
In-Place: Counting sort is not an in-place algorithm as it makes use of external memory
Stable: Counting sort can be both Stable and non-stable, the above algorithm is stable
Crisp Summery:
- Make assumptions about the data
- Doesn't use comparisons
- Counts the number of occurrences of each value
- Only works with non-negative discrete values (can't work with floats, strings)
- Values must be within a specific range.
- O(n) can achieve this because we're making assumptions about the data we're sorting.