Comparison-based Lower Bounds for Sorting
This article proves that there exists no possibility of having a Comparison-based sorting algorithm performs better than $O(nlogn)$
The Big question
When we look back and figure out that, all the comprassion based sorting algorithms such as
- Insertion Sort
- Mergesort
- Bubble sort
- Quick sort
- Selection sort etc.,
| Best Case Perfomance | Worst Case Perfomance | |
|---|---|---|
| Insertion Sort | $O(n)$ comprisions, $O(1)$ swaps | $O(n^2)$ comprisions and $O(1)$ swaps |
| Merge Sort | $O(n log n)$ | $O(n log n)$ |
| Bubble Sort | $O(n)$ comparisons, ${\displaystyle O(1)}$ swaps | $O(n^{2})$ comparisons, ${\displaystyle O(n^{2})}$ swaps |
| Quick Sort | $O(n log n)$ | $O(n^2)$ |
| Selection Sort | $О(n^2)$ comparisons, $О(n)$ swaps | $O(n^2)$ comparisons, $О(n)$ swaps |
There is no comprasion based sorting algorithm with time complexity less than $O(nlogn)$ in worst case. So what would be the lower bound of the comparsion based sorting algorithms
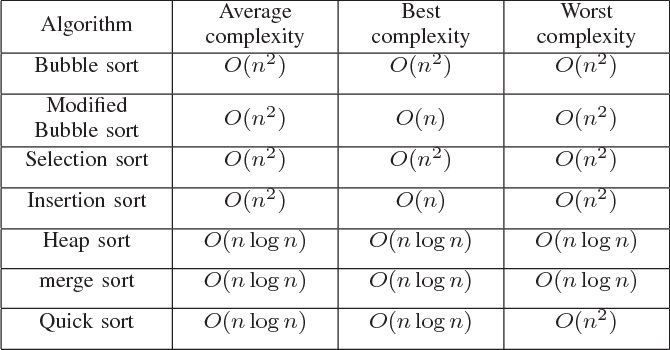
Imagine we have three elements $a_1, a_2, a_3$ in which $a_i \ne a_i$ and we are supposed to sort them in ascending order, The possible solutions would be
- $a_1, a_2, a_3$
- $a_1, a_3, a_2$
- $a_2, a_1, a_3$
- $a_2, a_3, a_1$
- $a_3, a_1, a_2$
- $a_3, a_2, a_1$
The possible ascending order would be one among these 6. Which means the number of outcomes is $n!$.The Number of ways we can arrange n elements in $n!$
Let's assume an abstract approach of a comparison-based sorting algorithm using a Binary Decision tree,
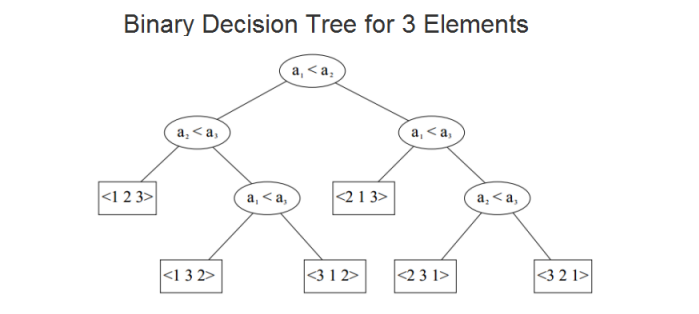
The possible arrangements of the three elements are the leaf nodes of the Binary Decision Tree. From this, we can say that the number of possible arrangements of n elements is equal to the number of leaf nodes in a binary decision tree.
Now, let's look into the hight of the tree. At each level of the tree we are making a decision, which means the height of the tree at a particular leaf will tell us the number of comparisons we made to reach that arrangement.
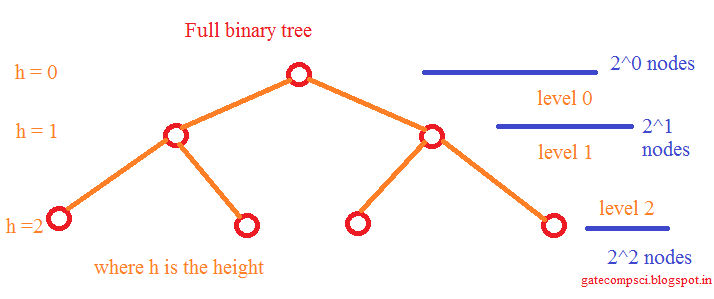
From the Full binary tree above we can say that the number of leaf nodes of this tree is $2^{height}$ and there is no possibility that the leaf nodes can more than $2^{height}$
Now, if we were given a binary decision tree for performing sorting which has $n!$[ref: Note2] leaf nodes, from the Note3, we can say that.
If h is the height of the Binary Decision tree that we are building for sorting n elements then,
$$2^{h} \geq n! $$
As the log is a monotonic function, we can apply log on both sides,
$$h \ge log(n!)$$
Now, we can calculate the h value which is the height, in return, we can figure out the comparison, from the asymptotic equations of growth of functions we know that,
$$log(n!) = \theta(nlogn)$$ $$log(n!) = \Omega(nlogn)$$
$$h = \Omega(nlogn)$$
Which means, the height of the binary decision tree for sorting n elements is lower bounded by $nlogn$, In which height is the number of comparisons we have to make.
From this we can say: