Problem Statement

Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.

Example 1: 

Input: 
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
Output: 
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

Example 2: 

Input: 
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
Output: 
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]

Follow up:

  • A straight forward solution using O(mn) space is probably a bad idea.
  • A simple improvement uses O(m + n) space, but still not the best solution.
  • Could you devise a constant space solution? [URL]

Approach 1 

#collapse-hide
from typing import List

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        temp = []
        matrixCopy = []
        
        for row in matrix:
            for element in row:
                temp.append(element)
            matrixCopy.append(temp)
            temp = []
            
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrixCopy[i][j] == 0:
                    for k in range(len(matrix[0])):
                        matrix[i][k] = 0
                    for k in range(len(matrix)):
                        matrix[k][j] = 0
        
        return matrix

sol = Solution()

sol.setZeroes([
  [1,1,1],
  [1,0,1],
  [1,1,1]
])

[[1, 0, 1], [0, 0, 0], [1, 0, 1]]

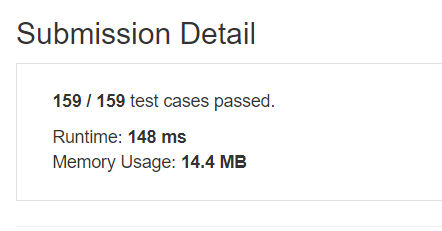
Worst case performance in Time: $O(m*n)$

Worst case performance in Space: $O(m*n)$

Is Inplace? : False

Approach 2

  1. Traverse the original matrix and look for 0 entities
  2. if found, record the i, j values using auxilary variables
  3. Using sets for recording i, j vlues would be benifiting as we overcome duplicate row, column values ahead.
  4. Finally, re iterate over the original matrix, for every cell make a check if i in rows or j in columns, update the values to 0.

#collapse-hide

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        rows = set()
        columns = set()
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrix[i][j] == 0:
                    rows.add(i)
                    columns.add(j)
        
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if i in rows or j in columns:
                    matrix[i][j] = 0
                    
        return matrix

sol = Solution()

sol.setZeroes([
  [1,1,1],
  [1,0,1],
  [1,1,1]
])

[[1, 0, 1], [0, 0, 0], [1, 0, 1]]

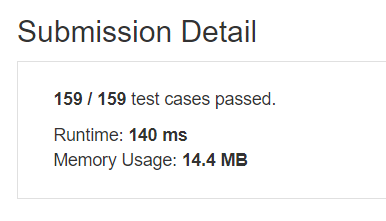
Worst case performance in Time: $O(m*n)$

Worst case performance in Space: $O(m+n)$

Is Inplace? : False

Approach 3 

#collapse-hide

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        rowFlag, colFlag = False, False
        
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if i == 0 and matrix[i][j] == 0:
                    rowFlag = True
                if j ==0 and matrix[i][j] == 0:
                    colFlag = True
                if matrix[i][j] == 0:
                    matrix[0][j] = 0
                    matrix[i][0] = 0
                    
        for i in range(1, len(matrix)):
                for j in range(1, len(matrix[0])):
                    if matrix[i][0] == 0 or matrix[0][j] == 0:
                        matrix[i][j] = 0
        
        if rowFlag == True:
            for i in range(len(matrix[0])):
                matrix[0][i] = 0
        if colFlag == True:
            for i in range(len(matrix)):
                matrix[j][0] = 0
        
        return matrix

sol = Solution()

sol.setZeroes([
  [1,1,1],
  [1,0,1],
  [1,1,1]
])

[[1, 0, 1], [0, 0, 0], [1, 0, 1]]

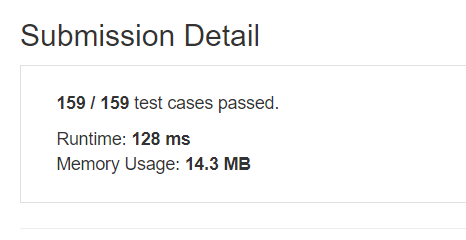
Worst case performance in Time: $O(m*n)$

Worst case performance in Space: $O(1)$

Is Inplace? : True