Problem Statement

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]). You are given a target value to find wheater the sum is possible from the array. If found in the array return True, otherwise return False.

You may assume no duplicate exists in the array.

Your algorithm's runtime complexity must be in the order of O(log n).

Example 1:

Input:
- nums = [9, 10, 11, 15, 26, 38]
- target = 35

Output: True

Example 1:

Input:
- nums = [9, 10, 11, 15, 26, 38]
- target = 45

Output: False

Approach 1:

Brute Force

works for any input array no matter of reversing and sorting

#collapse-hide
from typing import List

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        for i in range(len(nums)):
            rem = target - nums[i]
            for i in range(len(nums)):
                if nums[i] == rem:
                    return True
        
        return False

sol = Solution()
sol.search([2, 4, 1, 5, 6, 7, 8, 10], 12)

True

Worst case performance in Time: $O(n^2)$

Apprach 2:

If the input array is sorted

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        i = 0
        j = len(nums)-1
        while(i != j):
            if nums[i] + nums[j] == target:
                return True
            if nums[i] + nums[j] > target:
                j -= 1
            else:
                i += 1
        return False

sol = Solution()
sol.search([9, 10, 11, 15, 26, 38], 35)

True

sol = Solution()
sol.search([9, 10, 11, 15, 26, 38], 45)

False

If the array is sorted and rotated

Solution

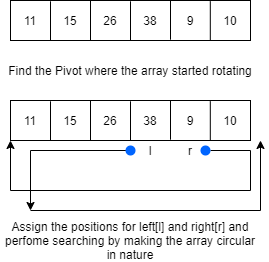
#collapse-hide
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, 0
        for i in range(len(nums)-1):
            if nums[i+1] < nums[i]:
                l = i+1
                r = i
                break
        while(l != r):
            if l == len(nums)-1:
                l = 0 
            if r == 0:
                r = len(nums)-1
                
            if nums[l] + nums[r] == target:
                return True
            if nums[l] + nums[r] > target:
                r -= 1
            else:
                l += 1
        return False

sol = Solution()
sol.search([11, 15, 26, 38, 9, 10], 35)

True

Twin

#collapse-hide
def pairInSorted(arr,s,n):
    for i in range(n-1):
        if(arr[i]>arr[i+1]):
            break
    l=(i+1)%n
    r=i
    
    while(l!=r):
        if(arr[l]+arr[r]==s):
            return True
        
        elif(arr[l]+arr[r]>s):
            r=(n+r-1)%n
        else:
            l=(l+1)%n
        
    return False
        
if __name__=='__main__':
    arr=[11, 15, 26, 38, 9, 10]
    s=19
    print(pairInSorted(arr,s,len(arr)))

True

Worst case performance in Time: $O(n)$