Introduction

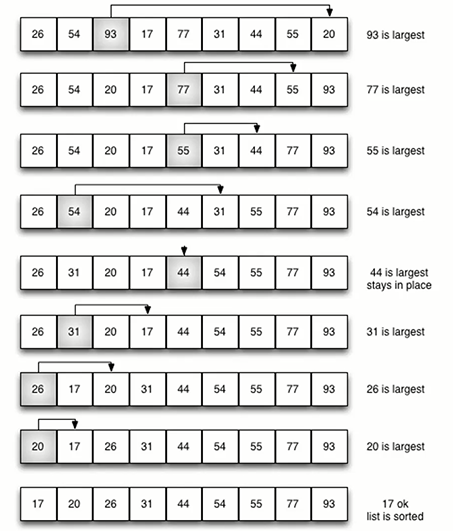
The selection sort can be implemented in two approaches by considering the largest elements or the smallest elements. Here we are considering the maximum elements sorting procedure.

The selection sort improves on the bubble sort by making only one exchange for every pass through the list.
A selection sort looks for the largest value as it makes a pass and, after completing the pass, places in the proper location.
After the first pass, the largest item is in the correct place. After the second pass, the next largest is in place.
This process continues and requires $(n-1)$ passes to sort $n$ items, since the final item must be in place after the $(n-1)st$ pass

Implementation of Selection Sort considering maximum elements

#collapse-hide
def selection_sort(arr):
    
    # For every slot in array
    for fillslot in range(len(arr)-1,0,-1):
        positionOfMax=0
        
        # For every set of 0 to fillslot+1
        for location in range(1,fillslot+1):
            # Set maximum's location
            if arr[location]>arr[positionOfMax]:
                positionOfMax = location

        temp = arr[fillslot]
        arr[fillslot] = arr[positionOfMax]
        arr[positionOfMax] = temp
        
        return arr

selection_sort(arr)

[1, 3, 5, 8, 10]

Algorithm

considering smallest elements

The algorithm proceedss by finding the smallest element in the unsorted subarrya
Exchange/ Swap it with the leftmost unsorted element -> putting it in sorted order
Moving the subarray boundaries one element to the right

Pseduocode

Implementation of Selection Sort considering minimum elements

#collapse-hide
def selectionSort(arr):
    for i in range(0, len(arr)-1):
        index = i
        
        for j in range(i+1, len(arr), 1):
            # For descending order use `>`
                if arr[j] < arr[index]:
                    index = j
        if index != i:
            arr[index], arr[i] = arr[i], arr[index]
    
    return arr

selectionSort(arr)

[1, 3, 5, 8, 10]

Crisp Info

Another $O(N^2)$ running time sorting algorithm
Selection sort is noted for its simplicity and it has perfomance advantages over more complicated algorithms
Particularly useful where auxiliary memory is limited.
The algorithm divides the input list into two parts:
- The subarray of items already sorted
- and the subarray of tiems remaining to be sorted that occupy the rest of the array
Quite counter-intutive: selection sort and insertion sort are both typically faster for small arrays [arrays with 10-20 items]
Makes less writes than insertion sort -> this can be important if writes are significantly more expensive than reads.
For example with EEPROM or flash memory where every write lessens the lifespan of the memory

Time Complexity [Worst Case]: $O(n^2)$

In Place Yes, as it don't require any extra memory

Stable No, does not reserve the order of keys with equal values